[목차]
수학 (상)의 2단원 첫 개념으로 다루게 될 내용은 복소수입니다. 복소수를 배우기 위해 필요한 개념은 고등학교 전의 내용으로, 이후 과정에는 다루지 않기 때문에 한번 짚고 가는 게 좋다 생각되어 포스팅하게 되었습니다. 이번 포스팅은 거듭제곱, 제곱근과 루트, 수의 체계에 대한 간단한 개념에 대해서 알아보겠습니다.
1. 거듭제곱
거듭제곱은 같은 숫자나 같은 문자를 여러 번 곱한 것을 간단히 표현한 것을 말합니다. 여기서 수학적으로 곱하게 되는 같은 문자를 밑, 곱한 횟수를 지수라고 칭합니다. 예를 들어, 만약 숫자 2를 5번 곱하면 2는 밑, 5는 지수가 됩니다.

같은 방법으로, 같은 문자 a를 n번 곱하는 경우에는 다음과 같이 일반화할 수 있습니다.

거듭제곱을 읽는 방법은 같은 문자(밑)를 두 번 곱한 경우(지수가 2) 일 때는 "(밑)의 제곱" 이라고 말하고, 그 외의 경우에는 밑과 지수를 보고 "(밑)의 (지수) 제곱"이라고 읽습니다. 즉, 보통의 경우 지수를 보고 2번 곱하면 제곱, 3번 곱하면 세제곱, 4번 곱하면 네제곱이라고 말하고 이후에는 오제곱, 육제곱, ... , 십제곱, 십일제곱 이런 식으로 읽습니다.
같은 의미로 제곱 대신 "승"이라고 읽기도 하는데요, 예를 들면 이승, 삼승, 사승, 오승, ... 과 같이 읽을 수 있습니다. 시대적으로 제곱이라는 말 이전에 승이라고 했지만, 최근에는 승이라는 말이 일본식으로 읽는 방법이라는 말이 돌고 있어 제곱이라고 읽는 것을 권한다고 합니다.

2. 제곱근과 루트
앞에서 어떠한 숫자 a를 두 번 곱하면 a의 제곱이라고 표현하는 것을 배웠습니다. a를 두 번 곱해서 나온 숫자를 x라고 하겠습니다. 여기서 제곱과는 반대로 a를 두 번 곱해서 x가 나올 때, 어떤 숫자 a를 x의 제곱근이라고 합니다.

위 식에서 제곱은 지수를 이용해 표현했다면, 제곱근은 "루트"라는 기호를 이용하여 표현하며, "제곱근 x" 혹은 "루트 x"라고 읽습니다.

간단하게 숫자로 이해해 보도록 하겠습니다.
만약 4의 제곱근을 구하라고 한다면, 제곱해서 4가 되는 숫자를 구하라는 말과 동일합니다. 이 말을 풀어서 한다면 같은 숫자를 두 번 곱했을 때 4가 되는 숫자가 무엇이냐?라고 해석할 수 있습니다. 4는 2를 두 번 곱하면 되므로, 2는 4의 제곱근입니다. 또한 음수 2를 두 번 곱하면 (-2)×(-2)=4이므로 -2도 4의 제곱근입니다. 따라서 4의 제곱근은 2, -2가 됩니다.
여기서 "x의 제곱근"과 "제곱근 x"에 대해서 헷갈려하시는 분들이 많으신데요. x의 제곱근은 같은 숫자 a를 두 번 곱했을 때 x가 나오는 a의 모든 값을 x의 제곱근이라 하며, 제곱근 x는 루트 x와 동일한 의미를 가지며 단순히 기호를 읽은 것입니다. 위 예시로 차이점을 본다면 4의 제곱근은 2, -2이며, 제곱근 4=루트 4=2입니다. 간단한 차이를 말하자면, x의 제곱근은 양수 제곱근과 음수 제곱근 모두를 포함하며, 제곱근 x는 양수 제곱근만 포함됩니다.

여기서 보통의 경우 제곱근을 구할 때 루트 안의 숫자가 양수지만, 양수가 아닌 음수가 루트 안에 있는 경우도 있습니다. 루트 안에 숫자가 음수인 경우는 다음에 배울 복소수의 개념에서 다루게 됩니다.
제곱근과 관련된 개념으로 거듭제곱근이라는 개념과 이를 계산하는 개념이 있는데 이는 수 1의 첫 단원인 지수와 로그에서 자세히 배우므로, 이번 포스팅에서는 복소수를 배우기 위해 필요한 개념만을 다뤘습니다.
3. 수의 체계
자연수, 소수, 정수와 같이 모든 숫자는 체계적으로 구별할 수 있습니다. 이처럼 숫자의 특성에 따라 구별한 것을 수의 체계라고 합니다. 각각의 용어에는 수학적인 정의가 있지만, 수학과 전공자가 아닌 이상 현 단계에서는 구별만 할 수 있으면 됩니다.
| 자연수 | 1, 2, 3, 4, 5, 6, ...과 같이 소수점이 없는 양수를 의미합니다. |
| 소수 | 자연수에 포함되며, 2, 3, 5, 7, ...과 같이 약수가 1과 자기 자신만 있는 수를 의미합니다. |
| 합성수 | 자연수에 포함되며, 2×2=4, 2×3=6 과 같이 두 개 이상의 숫자가 곱해진 수를 말하며, 동시에 소수가 아닌 숫자를 의미합니다. |
| 1은 소수도 아니며 합성수도 아닌 자연수입니다. | |
| 정수 | 자연수를 포함하며, 0을 포함한 소수점이 없는 음수와 양수를 의미하고 양의 정수, 음의 정수, 0으로 구분됩니다. |
| 양의 정수 | 자연수와 동일합니다. |
| 음의 정수 | -1, -2와 같이 자연수에 음의 부호 -를 붙인 수를 의미합니다 |
| 유리수 | 정수를 포함하며, 분모와 분자가 정수인 분수로 나타낼 수 있는 수를 의미합니다. 무한소수, 순환소수와 같은 숫자도 분수로 바꿀 수 있으니 유리수에 포함됩니다. |
| 무리수 | 유리수와 반대로 분모와 분자를 정수로 표현할 수 없는 숫자를 의미하며, 원주율 π, 자연상수 e, 루트 2, 루트 3과 같은 숫자가 포함됩니다. |
| 실수 | 위의 모든 수를 포함하며 실제로 존재하는 수 입니다. |
위 표에서 가장 범위가 큰 것은 모든 것을 포함하는 실수입니다. 실수의 설명에서 실제로 존재하는 수라고 설명되는 이유는 다음에 다룰 복소수가 실제 존재하는 수가 아닌 가상의 수를 포함하기 때문입니다. 자세한 내용은 다음 포스팅에서 다루겠습니다.
위의 표는 다음과 같이 다이어그램으로 표현할 수 있습니다.
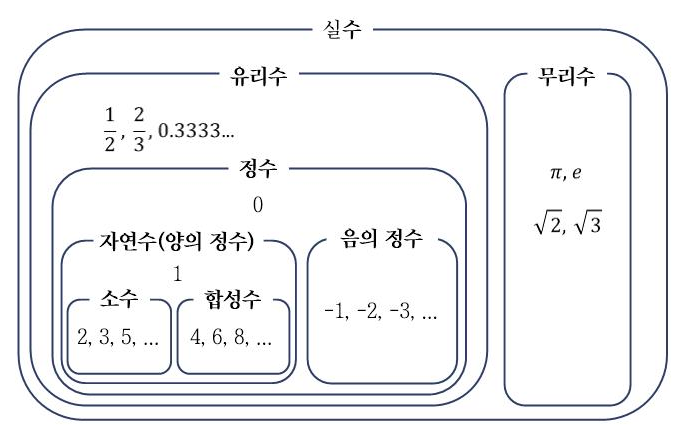
수의 체계는 훨씬 더 많이 세분화할 수 있습니다. 이번 포스팅에서는 가상의 숫자가 포함된 수의 체계를 배우기 전에, 실제 존재하는 숫자인 실수 범위까지의 수의 체계를 상기시키는 목적으로 알아보았습니다.
이번 포스팅은 거듭제곱, 제곱근과 루트, 수의 체계에 대해서 간단히 알아보았습니다. 고등학교 이전의 과정이기 때문에 자세한 내용을 다루지 않았기에, 이해가 되지 않는 부분은 댓글로 남겨주시면 보충하여 추가 수정하겠습니다.
'고등 수학 > 수학 (상)' 카테고리의 다른 글
| [수학 (상)] 2.3. 복소수의 연산 (0) | 2022.11.19 |
|---|---|
| [수학 (상)] 2.2. 허수와 복소수 (3) | 2022.11.17 |
| [수학 (상)] 1.9. 여러 가지 방법의 인수분해 (2) | 2022.11.08 |
| [수학 (상)] 1.8. 인수분해와 인수분해 공식 (0) | 2022.11.07 |
| [수학 (상)] 1.7. 나머지 정리, 인수 정리, 조립제법 (1) | 2022.11.02 |




댓글