[목차]
그래프는 함수를 눈으로 보고, 함수의 특징을 파악하고 분석하는데 도움을 주는 수학에서 유용한 도구로 활용됩니다. 이번 포스팅에서는 그래프에서 가장 기본 개념인 좌표와 좌표축에 관한 내용에 대해서 알아보겠습니다.
1. 좌표와 수직선 위의 좌표
[좌표]
좌표란 점의 위치를 나타내기 위한 값입니다. 점의 위치를 나타내기 위해서는 하나의 기준이 필요한데, 일반적으로 이 기준점을 원점이라고 합니다. 즉, 원점을 기준으로 점은 어디에 위치해 있는지를 값을 이용하여 나타내는 것을 좌표라고 합니다. 위치를 알고 싶은 점을 A라고 한다면, 원점에 대해서 앞에 있는지, 뒤에 있는지, 위에 있는지, 아래에 있는지, 또, 얼마나 떨어져 있는지와 같이 점의 위치를 부호와 값을 통해 나타낼 수 있습니다.

[수직선 위의 좌표]
원점에 대해서 점 A가 얼마나 떨어져 있는지는 두 점 사이의 길이를 통해 쉽게 알 수 있지만, 점 A가 원점의 뒤에 있는지 앞에 있는지는 알 수 없습니다. 그 이유는 원점에 대해서 어디가 앞인지, 뒤인지를 정의하지 않아서 인데요. 이를 정의하기 위해 도입된 것이 수직선입니다.
수직선은 하나의 긴 화살표를 긋고 기준점인 원점을 표시하여, 그 원점을 기준으로 점 A가 얼마나 떨어져 있는지와 원점의 앞에 있는지, 뒤에 있는지에 따라, +와 -기호로 나타낼 수 있습니다. 여기서 부호는 원점을 기준으로, 화살표가 가리키는 방향으로 점이 위치해 있으면 +, 반대 방향에 위치해 있으면 -로 나타냅니다. 일반적으로 수직선 방향은 왼쪽에서 오른쪽으로 가는 방향(→)을 +로 사용합니다. 원점은 기준점이기 때문에 위치와 거리가 없는 0의 값을 갖습니다.

예를 들어 점 A가 원점에서 2만큼 떨어져 있으면, 원점에서 화살표 방향으로 2만큼 떨어진 곳에 표시하고, 점 B가 원점에서 -3만큼 떨어져 있으면 화살표의 반대 방향으로 3만큼 떨어진 곳에 표시합니다. 여기서 수학적 기호로 점 A의 좌표는 A(2), 점 B의 좌표는 B(-3)으로 나타냅니다.

이를 일반화한다면, 임의의 점 P가 수직선 위의 원점에서 a만큼 떨어져 있을 경우, 기호로 P(a)로 나타냅니다.
2. 좌표축과 좌표평면
수직선 위의 좌표는 원점을 기준으로, 점 A가 앞에 있는지, 뒤에 있는지 값을 통해 알 수 있습니다. 점 A는 수직선 위의 원점의 앞과 뒤뿐만 아니라 수직선 밖의 위, 아래에 위치해 있을 수 있는데요. 이 경우, 앞/뒤와 마찬가지로 위/아래의 위치를 정의할 수 있는 또 하나의 축이 필요합니다. 따라서 위/아래의 방향을 나타내는 화살표를 추가하게 됩니다. 일반적으로 이 화살표는 아래에서 위로 가는 방향(↑)을 +로 사용하며, 원점을 지나도록 가로로 그려진 화살표에 대해 수직으로 그립니다.

화살표가 추가됨에 따라 두 개의 화살표 존재하게 되는데요. 이 두 개의 화살표를 좌표축이라고 하며, 각각의 방향을 구별하기 위하여 보통 가로 축은 x축, 세로 축은 y축으로 정합니다. 물론 x축과 y축은 필요에 따라 이름이 바꿀 수 있습니다.
이러한 두 개의 좌표축으로 인해 점 A는 앞/뒤와 위/아래의 위치를 나타낼 수 있습니다. 즉, 점 A는 선 위에서 뿐만 아니라, 두 개의 좌표축에 의해, 축 밖에 위치해 있어도 그 위치를 나타낼 수 있게 되는데요. 점 A의 위치를 표시할 수 있는 범위가 선 영역 벗어나 평면의 영역으로 확장되었다고 할 수 있으며, 이렇게 두 개의 좌표축으로 인해 생기는 영역을 좌표평면이라고 합니다.

예를 들어, 원점을 기준으로 점 A가 x축 방향으로 2만큼, y축 방향으로 3만큼 떨어져 있다면, 수학적 기호로 A(2, 3)으로 표시합니다. 또한 점 B가 x축 방향으로 -1만큼, y축 방향으로 -4만큼 떨어져 있다면, B(-1, -4)로 표시하며, 아래와 같이 위치를 나타낼 수 있습니다.
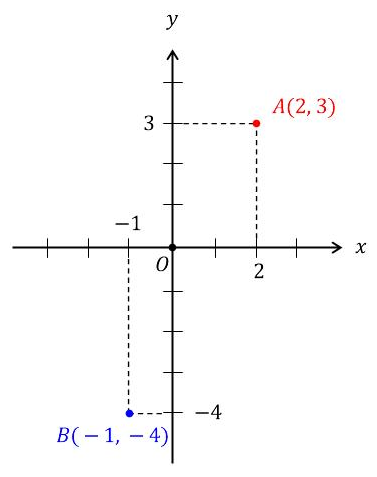
좌표의 수학적 기호는 대부분 약속되어 사용되는데요. 점의 좌표를 표시할 때 문자 옆의 괄호 안에는 가로 축인 x축 방향의 위치, 세로 축인 y축 방향의 위치를 순서대로 씁니다. 즉, A(x축 방향의 위치, y축 방향의 위치)으로 나타냅니다. 이를 일반화한다면, 임의의 점 P가 좌표평면 위의 원점에서 x축 방향으로 a만큼, y축 방향으로 b만큼 떨어져 있을 경우, 기호로 P(a, b)로 나타냅니다.
3. 사분면
사분면이란 좌표평면이 좌표축에 의해 4개의 영역으로 나뉜 것을 말합니다. 좌표평면 위의 점의 좌표가 +인지 -에 따라 점이 어떤 영역에 속해 있는지 구분할 수 있습니다. 4개의 영역으로 나뉘었기 때문에 사분면이라 하며, 각 영역을 제 1사분면, 제 2사분면, 제 3사분면, 제 4사분면으로 부릅니다. 각 사분면은 아래와 같은 조건에 따라 정의됩니다.
제 1사분면: x축의 좌표가 +, y축의 좌표가 +
제 2사분면: x축의 좌표가 -, y축의 좌표가 +
제 3사분면: x축의 좌표가 -, y축의 좌표가 -
제 4사분면: x축의 좌표가 +, y축의 좌표가 -
이를 좌표평면으로 보면 좌표축에 의해 나눠진 4개의 영역 중, 오른쪽 위의 영역을 제 1사분면으로 시작하여 반시계 방향으로 제 2사분면, 제 3사분면, 제 4사분면으로 나눠집니다.

예를 들어, A(1, 3), B(-1,-4), C(-2, 3), D(3, -2)의 4개의 좌표를 좌표평면에 표시하여, 각 점이 어떤 사분면에 있는지 직관적으로 알 수 있습니다.

따라서, 각 점이 위치한 사분면은 아래와 같습니다.
A: 제 1사분면 위의 점
B: 제 3사분면 위의 점
C: 제 2사분면 위의 점
D: 제 4사분면 위의 점
반대로 생각하면, 임의의 점 A(a, b)가
제 1사분면 위에 있으면 a>0, b>0
제 2사분면 위에 있으면 a<0, b>0
제 3사분면 위에 있으면 a<0, b<0
제 4사분면 위에 있으면 a>0, b<0
과 같은 조건을 가지는 것을 생각할 수도 있겠습니다.
만약 점이 특정한 사분면이 아니라 수직선 위에 있을 경우, 어떠한 사분면에도 속해있다고 하지 않습니다. 이 경우, 각 점이 속해 있는 축에 따라, x축 위에 있는 점, y축 위에 있는 점이라고 합니다. 예를 들어, 두 점의 좌표가 P(2, 0), Q(0, -3)라면, x축 위에 있는 점 P, y축 위에 있는 점 Q라고 부릅니다. A(0, 0)인 경우는 원점과 동일하기 때문에, 원점 위의 점이라고 할 수 있습니다.

'고등 수학 > 수학 (상)' 카테고리의 다른 글
| [수학 (상)] 2.6. 이차방정식의 근과 계수의 관계 (1) | 2023.01.29 |
|---|---|
| [수학 (상)] 2.5. 이차방정식의 해, 근의 공식, 판별식 (2) | 2022.12.12 |
| [수학 (상)] 2.4. 일차방정식의 해 (절댓값 기호가 있는 방정식) (0) | 2022.12.07 |
| [수학 (상)] 2.3. 복소수의 연산 (0) | 2022.11.19 |
| [수학 (상)] 2.2. 허수와 복소수 (3) | 2022.11.17 |




댓글